heappush()的参数 🔗

heapq.heappush(heap, item)有两个位置参数: heap 和 item , heap是堆的意思, item是要被压入到heap中的对象, 如果item无法通过小于号< 与heap中的各个元素进行比较, 那么就会报错

import heapq
heap = [1, 2, 3]
heapq.heappush(heap, 4)

结果:
此时heap变成了 [1, 2, 3, 4]

第一个位置参数heap 🔗

• heap的数据类型只能是一个列表, 如 heap = []
• heap中的元素如果符合heap[k]<=heap[k2+1]和heap[k]<=heap[k2+2], 那么这个heap就是一个堆, 或者说heap符合堆特性(heap property), 也可以说heap维持了堆的不变性(heap invariant.)
• 如果heap不符合堆的特性, 可以将heap传入heapq.heapify()进行堆化, 但前提是heap中的各个元素都可以使用小于号<进行比较运算,否则会报错, 字典类型是无法使用小于号进行比较运算的, 在heap中两个数据类型不同的元素也无法使用小于号进行比较运算,比如把整型值3和字符串’5’进行比较(3<‘5’)就会报错, 所以heap中元素的数据类型要相一致, 比如都是整型或者都是字符串型时,heapq.heapify()才能通过小于号比较heap中各个元素值以调整元素在heap中的顺序从而让其符合堆特性

第二个位置参数item 🔗

item的数据类型必须与heap中元素的数据类型相一致(item和heap中的元素的数据类型都不能是字典, 因为字典无法通过小于号进行比较运算.)比如heap中的元素都是整型值如[1, 2, 3], 那么使用heapq.heappush()压入到heap中必须是一个整型值(int类型), 比如heapq.heappush(heap, 8), 如果item不是整型值会报错, 比如heapq.heappush(heap, ‘8’) 会报错’<‘ not supported between instances of ‘str’ and ‘int’ 因为heappush需要使用小于号来比较插入到heap中的item和heap中原有元素的大小来调整heap中元素的顺序以满足堆特性(heap[k]<=heap[k2+1]和heap[k]<=heap[k2+2]),

堆特性 🔗

堆特性(heap property)也叫作堆的不变性(heap invariant).

最小堆 🔗

python里通常创建的是最小堆, 对于最小堆来说, 堆中索引位置0即heap[0]的值一定是堆中的最小值, 并且堆中的每个元素都符合公式heap[k] <= heap[k2+1]和 heap[k] <= heap[k2+2], 其中heap[k]是父节点, 而heap[k2+1]和heap[k2+2]是heap[k]的子节点, 父节点永远小于等于它自己的子节点, 这是不会改变的

最大堆 🔗

对于最大堆来说, 与最小堆相反, 堆中索引位置0即heap[0]的值是堆中最大值, 堆中每个元素都符合公式heap[k] >= heap[k2+1] 和heap[k] >= heap[k2+2], 父节点永远大于它的子节点, 这一点不会改变

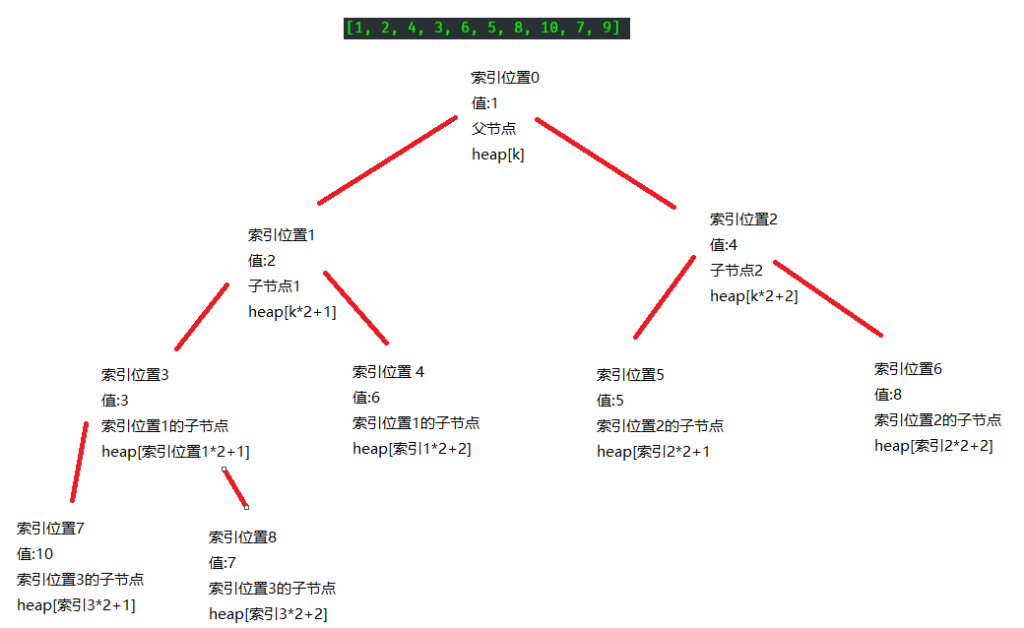
二叉树 🔗

堆是一个二叉树,从图中可以明白父节点heap[k]分出左右两个叉分别是

heap[k2+1]和heap[k2+2]

堆化 🔗

heapq.heapify() 🔗

如果一个列表中的所有元素数据类型相同并且各元素可以使用小于号进行比较运算, 那么这个列表就可以使用heapq.heapify()进行堆化

验证堆特性 🔗

只要列表中的所有元素都符合heap[k] <= heap[k * 2 + 1] 和 heap[k] <= heap[k * 2 + 2]即可, 父节点可以没有子节点, 如果没有子节点会报错IndexError, 所以需要处理异常

def check_heap(heap):
    for k in range(len(heap)):
        try:
            if heap[k] <= heap[k * 2 + 1] and heap[k] <= heap[k * 2 + 2]:
                print("符合 ", end="")
            else:
                print("不符合 ", end="")
            print('父节点索引位置' + str(k) + "小于等于", '子节点索引位置' + str(k * 2 + 1), '子节点索引位置' + str(k * 2 + 2))
        except IndexError:
            pass

heapq.heappush()维持堆的不变性 🔗

如果一个列表本身不符合堆(python里是最小堆)的特性, 比如heap = [7, 1, 8], 即使通过heap.heappush(heap, 4) 将整型值4压入heap, 这个heap最后也不会符合堆的特性. 如果一个列表本身就符合堆的特性或者个列表中的元素的个数小于等于1, 那么使用heapq.heappush()将值压入到这个列表后, 这个列表还是会符合堆的特性,维持了堆的不变性

import heapq
import random

heap = [10000, 100001, 100002]

for i in range(4):
    # 从0到1000之间随机调出一个整型值压入heap中
    heapq.heappush(heap, random.choice(range(1000)))
# 使用上面的函数验证一下是否符合堆的特性
check_heap(heap)
print(heap)

结果:
符合 父节点索引位置0小于等于 子节点索引位置1 子节点索引位置2
符合 父节点索引位置1小于等于 子节点索引位置3 子节点索引位置4
符合 父节点索引位置2小于等于 子节点索引位置5 子节点索引位置6
[333, 926, 511, 100001, 10000, 100002, 909]

升序的列表都符合堆的特性 🔗

如果一个列表中的元素数据类型一致(不包括字典), 并且使用升序排序, 那么这个列表就符合堆的特性, 比如 [0, 1, 2, 3], 因为一个升序列表意味着从小达到排列元素, 索引位置0的值一定是列表中的最小值,可以使用check_heap()验证.

如果一个列表可以使用列表的sort()方法排序(sort()方法在排序时也是需要使用小于号来比较各个元素的值), 排序后的列表也一定符合堆的特性,

heappush()的返回值 🔗

heapq.heappush()的返回值是None 也就是说没有返回值