最下层的三个点可以推导出上面的一切 🔗
汉诺塔的关键在于, 不管一共有多少层圆盘, 只要知道了最下层圆盘的行程轨迹, 就可以推导出上面所有圆盘的行程轨迹.
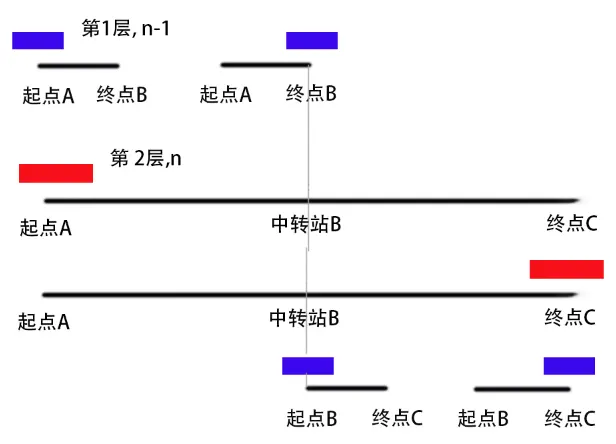
例如 hanoi(‘A’, ‘B’, ‘C’, 2), 第四个参数表示有两层圆盘, 前三个参数分别表示将下层的圆盘的起点设置为A, 终点设置为C, 中转站设置为B.
上层圆盘目标行程和下层一样, 也是要从A到移动到C, 所以上层的起点也是A, 终点也是C.
在两层圆盘移动时, 因为上层圆盘压着下层圆盘, 所以只能由上层先走, 而上层又不能直接走到终点C, 否则下层就永远无法到达C了, 所以上层决定先走到中转站B暂时停留, 把空间腾出来让下层直接从A走到C, 等下层到C后, 上层再从中转站B走到终点C.
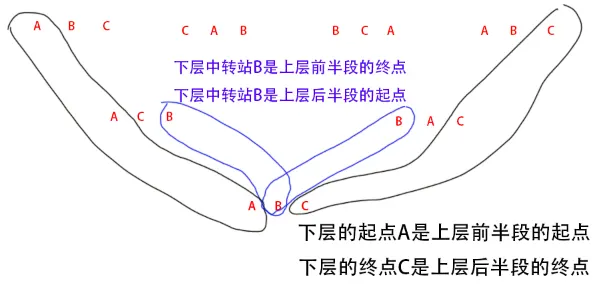
| 路程 | 起点 | 中转站 | 终点 |
|---|---|---|---|
| 上层前半段 | A | C | B |
| 下层 | A | B | C |
| 下层后半段 | B | A | C |
三层圆盘的汉诺塔 🔗
只要知道了下层圆盘行程的起点,中转站, 终点这三个点都是谁, 就能分别推导出它的上层分裂出的两个半程的行程的起点中转站和终点, 那么同理 如果上层还有上层, 也同样可以把行程推导出来. 假设有3层圆盘时, 第1层是最上面最小的圆盘,它和下面的第2层有构成的上下层的关系. 第2层圆盘的前半段的行程是从起点A走到终点B, 中转站是C, 即A,C,B , 那么第2层前半段上面的第1层的行程也是要从A走到B , 第1层将A到B的这一段行程也分成前后两段来走, 第2层前半段设置的中转站C就是第1层行程前半段的终点和第1层行程后半段的起点, 已知起点A, 终点C 那么第1层前半段的中转站就是B, 已知起点C终点B, 那第1层后半段的中转站就是A. 按照顺序排列:
| 路程 | 起点 | 中转站 | 终点 |
|---|---|---|---|
| 第1层前半段 | A | B | C |
| 第2层前半段 | A | C | B |
| 第1层后半段 | C | A | B |
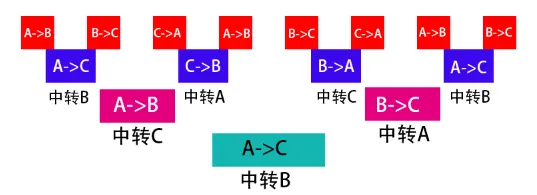
同理,对于第2层的后半段的路程, 第1层的圆盘也要把它分成两段来走, 按照这个比例关系, 最小的第1层圆盘要把最大的第3层圆盘的整段路程分成四段来走, 如下表
| 第几层 | 行走次数 | 路程 |
|---|---|---|
| 第1层,最小圆盘 | 4 | A->C, C->B, B->A, A->C |
| 第2层 | 2 | A->B, B->C |
| 第3层,最大圆盘 | 1 | A->C |
代码逻辑 hanoi(起点, 中转站, 终点, 第几层) 🔗
以下用python代码实现
# 起点 中转 终点 第几层
def hanoi(a, b, c, n):
if n == 1:
print(f"第{n}层圆盘从起点{a}走到终点{c}")
return
# 上层圆盘行程的前半程
hanoi(a, c, b, n-1)
# 下层圆盘的行程
print(f"第{n}层圆盘从起点{a}走到终点{c}")
# 上层圆盘行程的后半程
hanoi(b, a, c, n-1)
# 给汉诺塔整体行程设置起点终点,
# 整体的起点终点就是最下层的圆盘的起点和终点.
hanoi("A", "B", "C", 3)
当在全局调用hanoi()函数的时候, 实际上是在给汉诺塔最下层的圆盘的行程设置起点和终点, hanoi()的第四个参数n是几, 最下层的圆盘就是第几层.
hanoi()的前三个参数 🔗
比如在全局调用hanoi(‘A’, ‘B’, ‘C’, 3) 是在给汉诺塔第3层, 也就是最下层最大的那个圆盘设置起点和终点和中转站. 函数hanoi()前三个参数的意义:
- 第一个参数的意义是这里是起点, 当前将这里设置为A.
- 第二个参数的意义是这里是中转站. 当前将这里设为B,
- 第三个参数的意义是这里是终点, 当前将这里设置为C.
前三个参数的意义是不变的, 即使换了一套实参, 如 hanoi(‘C’, ‘A’, ‘B’, 5)也对应着(起点, 中转站, 终点), 即起点是C, 终点是B, 中转站是A.
hanoi()的第四个参数 🔗
第四个参数n, 除了表示一个有n层圆盘, 比如n=3时, 一共有3层圆盘. 除此之外它表示第n层圆盘, 比如第3层圆盘(最下层), 第3层圆盘上一层是第2层圆盘, 所以第2层圆盘可以表示为n-1. 所以在函数hanoi()中递归调用自己传入的hanoi(a, c, b, n-1)其实是在给当前这一层圆盘的上一层(n-1层)设置行程起点和终点.
hanoi()的递归调用 🔗
在hanoi()内遇到的第一个递归调用hanoi(a, c, b, n-1) 表示是在给上层(当前层是n, 上层就是n-1)圆盘的前半程设置起点和终点, 可以看到参数列表里是a, c, b, 也就是当前层(第n层)里存储着起点信息的变量a还同时是上层(n-1)前半程的起点的位置, 而存储当前层(n)中转站信息的变量b跑到了上层(n-1)前半程的终点位置, 存储着当前层(n)终点信息的变量c跑到了上层(n-1)前半程的中转站位置. 如果n不等于1的话, 那么就会无限的递归下去, 每递归调用一回n都会减少1, 直到n==1. 当n==1时, 表示已经来到了所有圆盘的最上层, 也就是第1层圆盘, 当执行print语句后, 必须使用return语句退出当前第1层圆盘的递归调用, 从而回到第2层圆盘, 否则不用return退出而继续向下执行就会进入死循环.当能从第1层正常退出回到第2层后, 遇到了print语句, 打印”第2层圆盘从起点A走到终点B”, 然后又遇到了第二次递归调用hanoi(b, a, c, n-1), 同理这是在给上一层圆盘的后半程设置起点终点.
上面的章节说了, 只要知道下层行程的3个点, 就能通过这三个点推导出来上层的前半段行程的三个点,和上层后半段行程的三个点, 其实当在递归调用hanoi(a, c, b, n-1)的时候传入那的那三个变量a,c,b, 其实已经变成了新的下层, 随之进入的递归调用的函数体内又遇到的两次新的递归调用里传入的参数a,b,c和c,a,b,实际上就是由新下层a,c,b推导出来的新的上层前半程和后半程, 如此往复.
挪动次数的公式 🔗
如果共有4层圆盘, 第4层最大的圆盘只走1段路程, 第3层把第4层一段路程当成两段来走, 也就是说上层的行走次数一定是下层的2倍, 如此类推,第2层就是2×2, 第1层就是2x2x2, 最后得到 1+2+2×2+2x2x2=15 , 而15正好等于2的四次方-1, 所以可以归纳出n层圆盘从A点走到C点的行走次数是 (2^n)-1 , 如下图4层圆盘行走次数成倒金字塔的形状
| 总次数 | 等于 | ||
|---|---|---|---|
| 共1层 | 1 | 1 | 2^1 – 1 |
| 共2层 | 1 + 2 | 3 | 2^2 – 1 |
| 共3层 | 1 + 2 + 2×2 | 7 | 2^3 – 1 |
| 共4层 | 1 + 2 + 2×2 + 4×2 | 15 | 2^4 – 1 |
用循环实现汉诺塔 🔗
使用循环的方式来实现汉诺塔, 和递归的方式有个共同点, 就是还是通过下层行程的三个点来推导出上层前半段和后半段的行程各三个点. 不同点是循环的方式需要提成生成好一张所有圆盘所有行程的表, 然后再生成一张行程行走先后顺序的表, 配合两个表才能按正确顺序打印输出这n层圆盘都是怎么移动的, 比如代码:
n = 5
# 按照每层圆盘的行走顺序存储行程
travel_map = dict()
# 设置最下层圆盘的起点A, 中转站B, 终点C
travel_map[n] = [["A", "B", "C"]]
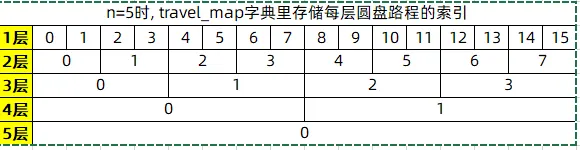
# n=5时, travel_map中存储行程索引如下
# [0, 1, 2, 3]
# [0, 1]
# [0]
# 以travel_map中的索引在i_map中生成正确行程顺序的索引, 如下:
# [3, 11, 19, 27]
# [7, 23]
# [15]
index_map = dict()
final = dict()
def hanoi_top(a, b, c):
# 返回的是上层圆盘行程前半段的起点和终点, 以及后半段的起点和终点
return [[a, c, b], [b, a, c]]
def make_index_map(n):
for i in range(1, n + 1):
index_map[i] = []
# 某层的行首索引位置为0的路程对应的正确行程的索引
first = pow(2, i - 1) - 1
index_map[i].append(first)
# 推导式不好理解, 保留
# index_map[i].extend(
# [first + pow(2, i) * (k + 1) for k in range(pow(2, n - i) - 1)]
# )
# pow(2, n - i)是当前层圆盘行程的数量, n=5时, 第一层是16段行程, range(16-1) == 0~15
for k in range(pow(2, n - i) - 1):
# 当前层圆盘每段路程之间的索引间隔数, 比如n=5时, 第1层圆盘第一段行程正确行走的索引是0,
# 第二段路程的正确行走索引就是0+2的1次方即0+2, 所以是0
first += pow(2, i)
# 比如n=5时, 第1层16段路程正确行走的索引是[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30]
index_map[i].append(first)
def navigator(dravel_map, n):
make_index_map(n)
for i in dravel_map:
for k, v in enumerate(dravel_map[i]):
# 行程正确行走顺序对应final的索引, 比如行程正确顺序是第15步 对应 final[14]
final[index_map[i][k]] = v
def make_travel_map():
# 比如第5层开始遍历, 最高层是1,
# 这里不会遍历到最高层, 只会遍历到次高层, 因为在次高层的时候已经生产出了最高层的行程路线了.
# 比如 range(5, 1, -1) 实际只会遍历4次, 分别是5, 4, 3, 2,
# 因为在第2层圆盘所处的循环中会使用hanoi_top制造第1层圆盘行程并存储在第1层圆盘的列表里
for i in range(n, 1, -1):
# 初始化存储当前层的上一层圆盘行程的列表, 比如 当前层是第5层, 上一层就是第4层
travel_map[i - 1] = []
# 遍历当前层的行程列表
for k in travel_map[i]:
# 因为当前层的一段行程, 其上层要分成两段走, 即当前层的一段行程会延伸出上层的两段行程
# 通过hanoi_top制作出以当前层某段行程为基础延伸出上层的两段行程, 并将该两段行程存储到上层列表i-1中,
travel_map[i - 1].extend(hanoi_top(*k))
# 依据最下层ABC三个点制作n的行程地图存储在travel_map中
make_travel_map()
# 依据正确行程顺序的索引index_map把值存储在final里
navigator(travel_map, n)
# final是乱序的, 需要sorted排序一下
for i in sorted(final):
print(f"第{i+1}步: 从起点{final[i][0]}走到终点{final[i][2]}")
上面的python代码中:
-
travel_map[n] = [[“A”, “B”, “C”]] 表示用来设置最下层圆盘的行程, 等价于hanoi(“A”,”B”,”C”,n)
-
函数hanoi_top(a, b, c) 接受的参数是下层圆盘传入的行程的3个点, 然后用这个3个点推导出上层圆盘前半段行程的三个点, 和后半段三个点
-
make_travel_map()函数通过hanoi_top()以最下层的行程推导出所有的行程, 并将所有行程存储在字典travel_map
-
-
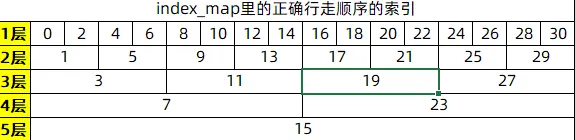
travel_map里的索引并不是圆盘行走的正确顺序, 比如第1层圆盘不可能把自己16段行程都走完后, 第2层再走自己的8段行程. 所以通过自己推演推算每一步行程的先后顺序, 可以推算出在travel_map对应的从第1步直到最后一步的正确行程行走顺序的索引表如下:
-
-
通过index_map这张表可以发现, 在第1层里每个索引号之间都差了2, 2可以表示为2的1次方, 第2层每个索引号之间都差了4即2的2次方,所以每个的索引号之间的规律是都相差了2^i, i是当前所在的第几层.所以如果要是还能知道每行行首的索引就能推算出所有的正确索引号了, 可以发现每行行首的规律都是2^(i-1)-1, i是在第i层, 比如第4层圆盘2^(4-1)-1=7, 所以第4层的行首索引是7
-
通过make_index_map()函数依据横向规律2^i和纵向规律2^(i-1)-1可以计算出正确行走顺序索引表存储在字典index_map里, 无论多少层圆盘.
-
navigator()函数使用通过字典index_map和字典travel_map的对应关系将每段行程配以正确行走顺序的索引存储在字典final里, 比如 某段行程因该是第25步, 那么会将这段行程存储在final[24]里, 索引是从0开始.
-
final里的索引是乱序的, 在遍历的时候需要用sorted排序一下